CCLM: CLass-Conditional Label Noise Modelling

Sunday. June 25, 2023 - 3 mins

Published @IbPRIA and awarded the Best Paper Award. Here for the complete paper.

Why?

Learning with Noisy Labels (LNL) is concerned with training models when the data sample, label pairs are potentially noisy. In a future where this problem is solved, one could leverage search engines, low-fidelity tagging systems like social networks… to create gigantic datasets and actually learn from them.

How?

The current training pipline in LNL is to model the sample label noise, and then according to what is the resulting probability of a sample being noisy, the dataset is split into the hopefully mostly clean set and the hopefully mostly noisy set. Afterwards, a flavour of semi-supervised learning is used to take advantage of the data available.

So…?

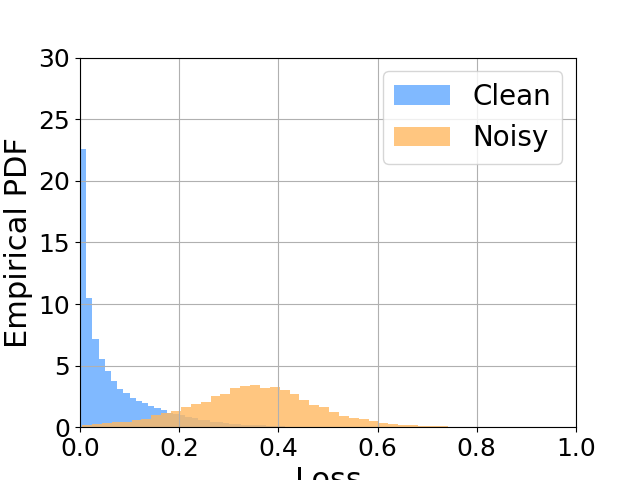
Our paper focuses on the Label Noise Modelling step. It is known that there is a simplicity bias¹ in Deep Learning, and often believed that it is one of the key reasons that makes it work so well. In label noise modelling, we try to take advantage of it. The model is trained conventionally for some epochs (~10 for CIFAR-10), called the warm-up phase. Afterwards, we hope that the model has learned a “meaningful representation” but it hasn’t memorized the noise in the data, it is known that networks learn easier patterns first, and then more complex ones (similar to what is going on in the .gif). Finally, with the warmed-up network, it is typically assumed that all the loss of all the samples follow a bi-modal normal distribution. Thus, in the modelling phase, we fit a 2-mode Gaussian Mixture Model to extract the two sub-pupulations. The idea behind it is that the sub-population with higher loss is going to have the noisy samples (the network hasn’t had time to learn the complex noise yet), and the sub-pupulation with lower loss is going to be mostly clean. Then with a hyperparameter threshold, we split the data according to these probabilities, and follow along with semi-supervised learning. This process is repeated at every epoch. The following image illustrates the sample loss distribution. We can see that the core assumption we made is reasonable.

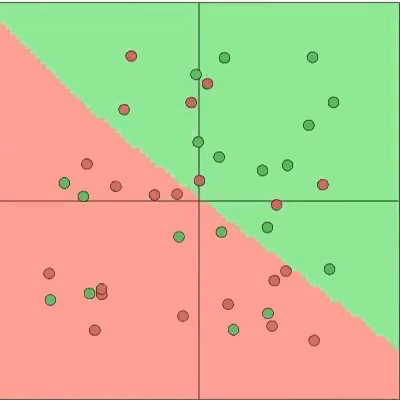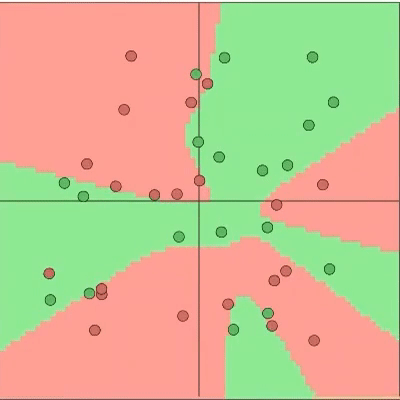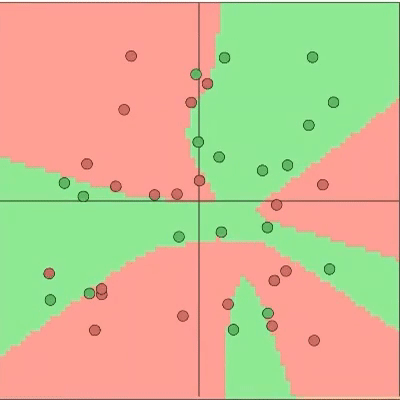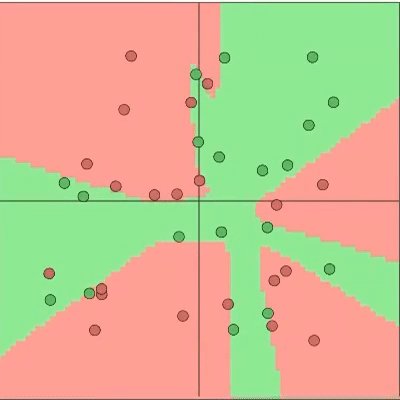
Our proposal

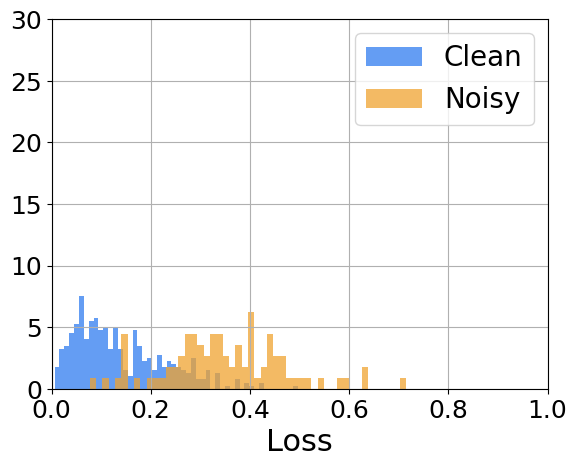
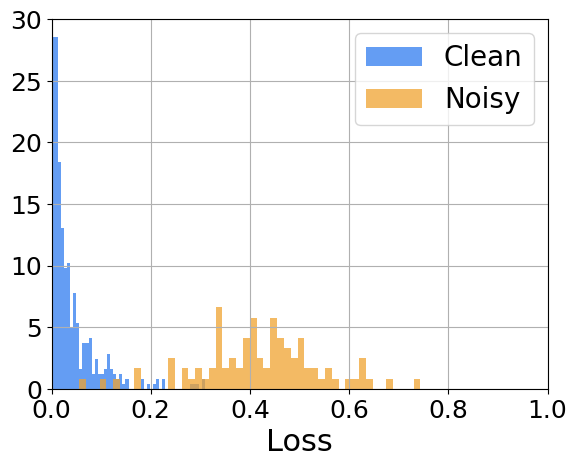
We realize that there are some classes that are harder to learn than others. How would that affect the loss as an indicator of sample cleanliness? Our proposal is to change the assumption that all the samples follow a bi-modal normal distribution with all the samples of a class follow a bi-modal normal distribution, which can be different for every class. You might be scratching your head now, what does “class” mean?? In this context, a class is a group of samples with the same (potentially noisy) label. The two following pictures help showcase how the proposed assumption is less constraining and more realistic.

Results

In the paper we show how our extremely simple proposal improves classification accuracy, and other interesting metrics such as classiness, defined as the standard deviation of the accuracy over the classes.